|
|

楼主 |
发表于 30-7-2005 10:02 PM
|
显示全部楼层
最近真的是忙透了。。。
也许迟些再上来与大家玩玩!
(忙归忙,倒感觉挺充实的 ) ) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-11-2005 02:34 PM
|
显示全部楼层
发表于 21-11-2005 02:34 PM
|
显示全部楼层
对不起, 请问你们在讨论的数学是哪一个阶级的?
我对这个有点兴趣,是想学额外的数学啦。但本人现在只是个在学院修读大学基础班的学生。
学这个会不会太不自量了? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-11-2005 04:10 PM
|
显示全部楼层
发表于 21-11-2005 04:10 PM
|
显示全部楼层
|
只要有兴趣就可以了。这其实是一些 olympiad standard 的题目。大学如果修读数学系的话应该也有读吧。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-11-2005 01:26 AM
|
显示全部楼层
发表于 26-11-2005 01:26 AM
|
显示全部楼层
趣味不等试
若 a,b,c >0证明
sqrt {a^2-ab+b^2} + sqrt{b^2-bc+c^2} => sqrt{a^2+ac+c^2} |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-1-2006 03:36 PM
|
显示全部楼层
发表于 4-1-2006 03:36 PM
|
显示全部楼层
Junior Balkan MO 2002 :
a,b,c 为正实数,试证明
1/a(a+b) + 1/b(b+c) + 1/c(c+a) >= 27/[2(a+b+c)^2]
注:有个很美丽的解,只用AM-GM 和 AM-HM 吧了!
[ 本帖最后由 dunwan2tellu 于 5-1-2006 02:38 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-1-2006 09:58 PM
|
显示全部楼层
发表于 4-1-2006 09:58 PM
|
显示全部楼层
我看不明白....
第二楼的......
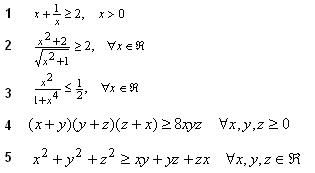
右边的是答案吗?? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-1-2006 10:39 PM
|
显示全部楼层
发表于 4-1-2006 10:39 PM
|
显示全部楼层
是条件,不是答案 ....比如第一题
当x>0 时,x+1/x >2 .... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-1-2006 10:11 PM
|
显示全部楼层
发表于 5-1-2006 10:11 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 4-1-2006 10:39 PM 发表
是条件,不是答案 ....比如第一题
当x>0 时,x+1/x >2 ....
x+1/x>2
x+1>2x
x<1
是酱吗??
还有很多符号我看不懂......
那个很像反回来的A是什么....=.= |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-1-2006 02:44 PM
|
显示全部楼层
发表于 6-1-2006 02:44 PM
|
显示全部楼层
原帖由 kjying 于 5-1-2006 10:11 PM 发表
x+1/x>2
x+1>2x
x<1
是酱吗??
还有很多符号我看不懂......
那个很像反回来的A是什么....=.=
不是。。。
这问题是要证明不等式。。
只需用AM-GM就可以了 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-1-2006 03:35 PM
|
显示全部楼层
发表于 6-1-2006 03:35 PM
|
显示全部楼层
哈哈哈,摆了个大乌龙。。。
saddam2006是我的朋友,我竟然用了他的会员名字来回帖。。。
(x + 1/x)/2 >= [x(1/x)]^(1/2)
x+1/x >= 2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-1-2006 07:37 PM
|
显示全部楼层
发表于 6-1-2006 07:37 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-1-2006 04:44 PM
|
显示全部楼层
发表于 9-1-2006 04:44 PM
|
显示全部楼层
用AM-GM
1/a(a+b) + 1/b(b+c) + 1/c(c+a) >= 3 X [1/abc(a+b)(a+c)(b+c)]^(1/3)
用GM-HM
[1/abc]^(1/3) >= 3/(a+b+c)
[1/(a+b)(b+c)(c+a)]^(1/3) >= 3/2*(a+b+c)
得1/a(a+b) + 1/b(b+c) + 1/c(c+a) >= 27/2*(a+b+c)^2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-1-2006 05:35 PM
|
显示全部楼层
发表于 9-1-2006 05:35 PM
|
显示全部楼层
原帖由 hamilan911 于 9-1-2006 04:44 PM 发表
用AM-GM
1/a(a+b) + 1/b(b+c) + 1/c(c+a) >= 3 X [1/abc(a+b)(a+c)(b+c)]^(1/3)
用GM-HM
[1/abc]^(1/3) >= 3/(a+b+c)
[1/(a+b)(b+c)(c+a)]^(1/3) >= 3/2*(a+b+c)
得1/a(a+b) + 1/b(b+c) + 1/ ...
对了!就是酱!可以试试前几题 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-1-2006 09:57 AM
|
显示全部楼层
发表于 14-1-2006 09:57 AM
|
显示全部楼层
|
对不起,冒然打扰...想请教大家,怎样直接在casio fx-570W 的计算机,解三次方的功式?eg. x^3 + 8x^2 + 20x + 20... 十万火急,望大家能伸出援手,谢谢! 小弟电邮为 no7_alfred@hotmail.com |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-1-2006 11:48 AM
|
显示全部楼层
发表于 14-1-2006 11:48 AM
|
显示全部楼层
Mode-EQN-Degree3
ax^3+bx^2+cx+d=0
输入a,b,c,d即可。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-1-2006 07:03 PM
|
显示全部楼层
发表于 14-1-2006 07:03 PM
|
显示全部楼层
|
我在 FX-570W 的 MODE 里找不到 EQN 的 function... T_T |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2006 10:01 PM
|
显示全部楼层
发表于 16-1-2006 10:01 PM
|
显示全部楼层
原帖由 hamilan911 于 9-1-2006 04:44 PM 发表
用AM-GM
1/a(a+b) + 1/b(b+c) + 1/c(c+a) >= 3 X [1/abc(a+b)(a+c)(b+c)]^(1/3)
用GM-HM
[1/abc]^(1/3) >= 3/(a+b+c)
[1/(a+b)(b+c)(c+a)]^(1/3) >= 3/2*(a+b+c)
得1/a(a+b) + 1/b(b+c) + 1/ ...
题目是X...
做么有ABC出来的......=.= |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2006 10:59 PM
|
显示全部楼层
发表于 16-1-2006 10:59 PM
|
显示全部楼层
原帖由 kjying 于 16-1-2006 10:01 PM 发表
题目是X...
做么有ABC出来的......=.=
我证明的是以下这题
1/a(a+b) + 1/b(b+c) + 1/c(c+a) >= 27/[2(a+b+c)^2] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-2-2006 03:13 PM
|
显示全部楼层
发表于 9-2-2006 03:13 PM
|
显示全部楼层
不难的不等式:
若 m 是正整数,证明
1/(m+1) + 1/(m+2) + 1/(m+3) + ... + 1/[m+(2m+1)] > 1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-2-2006 09:50 PM
|
显示全部楼层
发表于 10-2-2006 09:50 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 9-2-2006 03:13 PM 发表
不难的不等式:
若 m 是正整数,证明
1/(m+1) + 1/(m+2) + 1/(m+3) + ... + 1/[m+(2m+1)] > 1
i)AM-HM
1/(m+1) + 1/(m+2) + 1/(m+3) + ... + 1/[m+(2m+1)]/(2m+1)
>= (2m+1)/[m+1+m+2+m+3...+m+2m+1]
>= (2m+1)/[(2m+1)m + (2m+1)(2m+2)/2 ]
>= (2m+1)/(2m+1)^2
>= 1/(2m+1)
所以1/(m+1) + 1/(m+2) + 1/(m+3) + ... + 1/[m+(2m+1)] > 1
(equality hold when 1/(m+1) = 1/(m+2),而这情况是不可能的)
ii)用jensen
f(m)= 1/(m+1) f''(m) = 2/(m+1)^3 > 0
[f(1)+f(2)+f(3)+...+f(2m+1)]/(2m+1) >= f[(1+2+3+...2m+1)/(2m+1)]
>= f[m+1]
[f(1)+f(2)+f(3)+...+f(2m+1)] >= (2m+1)f[m+1] = (2m+1)/(2m+1) = 1
所以1/(m+1) + 1/(m+2) + 1/(m+3) + ... + 1/[m+(2m+1)] > 1
(equality hold when 1/(m+1) = 1/(m+2),而这情况是不可能的)
[ 本帖最后由 hamilan911 于 11-2-2006 02:46 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|