prove limit

s501aw

Prove an is convergent, where x is real number .



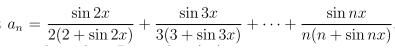
高手请指点迷津， 如何运用epsilon-N 来prove ? 或其他方法。

dunwan2tellu

先证明 |sin nx / (n(n+ sin nx))| =< 1/n(n-1) （提示用triangle inequality 和 |sin nx| =< 1)

然后 证明 |a_n| converges abosolutely (提示：需要用 1/n(n-1) = 1/(n-1) - 1/n)

用的 concept 基本上是 telescoping series 如何加起来的 concept

s501aw

|(n+ sin nx)| =< |n| + |sin nx| =< n+1

过后， reciprocal 应该是  1/ |(n+ sin nx)| => 1/(|n| + |sin nx|) =>1/( n+1)


|sin nx / (n(n+ sin nx))| >= 1/n(n+1)

这是我得到inequality  那里有问题？

dunwan2tellu

用另一个 triangle inequality

|a+b| >= |a| - |b|

s501aw

有了。 ok.