|
|
 发表于 6-5-2010 09:17 PM
|
显示全部楼层
发表于 6-5-2010 09:17 PM
|
显示全部楼层
to determine the root of
12x^4+20x^3-11x^2-5x+2=0
dy/dx = 48x^3 +60x^2 -22x -5
using ...
白羊座aries 发表于 6-5-2010 08:58 PM 
不需要吧。。。太长了。。。直接猜一个ROOT。。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 09:38 PM
|
显示全部楼层
发表于 6-5-2010 09:38 PM
|
显示全部楼层
Prove without using a calculator, that
(a) 2
Lov瑜瑜4ever 发表于 6-5-2010 07:40 PM 
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 09:44 PM
|
显示全部楼层
发表于 6-5-2010 09:44 PM
|
显示全部楼层
回复 1035# Lov瑜瑜4ever

2<t<3
2-2<t-2<3-2
0<t-2<1

(square root of + 2)^4 > 321想不到, 另请高明吧.. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-5-2010 03:35 PM
|
显示全部楼层
发表于 7-5-2010 03:35 PM
|
显示全部楼层
噢噢噢。。。
Lov瑜瑜4ever 发表于 6-5-2010 09:13 PM 
this question got 3 method to solve
1)by guessing one of the root(walrein show already)
2)newton-rapston(show already)
3)iriteration(by using graph to find one of the root)
method 1 is fastest if you guess the integer correctly,method 2 is more complicated and never reach the correct answer(approximately),method 3 is the most "laoya" one method,so i do not want to show... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-5-2010 04:00 PM
|
显示全部楼层
发表于 7-5-2010 04:00 PM
|
显示全部楼层
this question got 3 method to solve
1)by guessing one of the root(walrein show already)
...
语曦 发表于 7-5-2010 03:35 PM 
我都用第一个方法的
第一个方法也是我最早学到的方法
比较熟
ohorhor |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-5-2010 04:52 PM
|
显示全部楼层
发表于 7-5-2010 04:52 PM
|
显示全部楼层
回复 1045# Lov瑜瑜4ever
trial and error |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-5-2010 11:38 PM
|
显示全部楼层
发表于 7-5-2010 11:38 PM
|
显示全部楼层
Given that 11x^2-8xy+5y^2=32
x^2+y^2=8
deduce that 7x^2-8xy+y^2=0,and, hence, find all the pairs of values of x,and y that satisfy the given equation.(这题我已解答了,只是有几个疑问而已)
我的解答方法:
step 1: 11x^2-8xy+5y^2=32-------1
x^2+y^2=8--------2
1/2 11x^2-8xy+5y^2/x^2+y^2=32/8
32x^2+32y^2=88x^2-64xy+40y^2
0=56x^2-64xy+8y^2
0=7x^2-8xy+y^2
ps:(我想知道为什么要用1除2,因为我的书里没解释)
step 2: 7x^2-8xy+y^2=0
(7x-y)(x-y)=0
x=y/7 x=y
step 3: If x=y/7 x^2+y^2=8
y^2/49+y^2=8
y^2+49y^2=392
y^2=196/25
y=+14/5 or -14/5
if y=14/5 x^2+(14/5)^2=8 if y=-14/5 x^2+(-14/5)^2=8
x^2+196/25=8 x^2+196/25=8
25x^2+196=200 25x^2+196=200
25x^2=4 25x^2=4
x^2=4/25 x^2=4/25
x=2/5,-2/5 x=2/5,-2/5
书里的答案只有(2/5,14/5)和 (-2/5, -14/5),但是没有(2/5, -14/5) 和(-2/5,14/5),为什么后面两个不能呢?
step 4 :if x=y if y=2 if y=-2
x^2+y^2=8 x^2+2^2=8 x^2+(-2)^2=8
2y^2=8 x^2=4 x^2=4
y^2=4 x=2,-2 x=2,-2
y=2,-2
一样的书的答案是(2,2)和(-2,-2)而没有(2,-2)和(-2,2),为什么? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-5-2010 08:22 AM
|
显示全部楼层
发表于 8-5-2010 08:22 AM
|
显示全部楼层
Given that 11x^2-8xy+5y^2=32
x^2+y^2=8
deduce that 7x^2-8xy+y^2=0,and, hence, find ...
blazex 发表于 7-5-2010 11:38 PM 
如果你用1的eq除以2的eq的话就能都deduce到题目要得equation
而且题目要你deduce的equation是能够factorise的
其实要除就是因为能够让2个eq变成一个可以被factorise的eq咯
至于接下来的问题
我就不懂了
我的书本是2个都接受
不管是+还是-
但是题目和你不一样。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-5-2010 01:28 PM
|
显示全部楼层
发表于 8-5-2010 01:28 PM
|
显示全部楼层
Given that 11x^2-8xy+5y^2=32
x^2+y^2=8
deduce that 7x^2-8xy+y^2=0,and, hence, find ...
blazex 发表于 7-5-2010 11:38 PM 

应该两个都被接受。。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-5-2010 11:04 PM
|
显示全部楼层
发表于 8-5-2010 11:04 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-5-2010 12:26 PM
|
显示全部楼层
发表于 9-5-2010 12:26 PM
|
显示全部楼层
it is given that f(x)=x^n-nx+n-1 for the interger n>1.
By considering f(x) and f'(x),show that
f(x)=(x-1)^2g(x)
is true for all polynomial g(x) with integer coefficients.
Hence, show that 3^2n-8n-1 is divisible by 64 for all integers n>1
当证明一个问题时可以只用一个句子解释吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-5-2010 11:24 AM
|
显示全部楼层
发表于 10-5-2010 11:24 AM
|
显示全部楼层
it is given that f(x)=x^n-nx+n-1 for the interger n>1.
By considering f(x) and f'(x),show that
...
blazex 发表于 9-5-2010 12:26 PM 
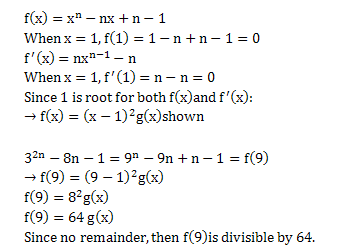 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-5-2010 01:28 PM
|
显示全部楼层
发表于 15-5-2010 01:28 PM
|
显示全部楼层
sequences and series:method of difference
到底怎么做啊?我一点idea也没有~
例如这题要怎么做呢?
show that f(r) = 1/(2r+1)(2r+3) then f(r)-f(r-1) = -4/(2n-1)(2n+1)(2n+3). Hence, or otherwise, find the sum of the series.
1/1x3x5 + 1/3x5x7 + 1/5x7x9 + 1/7x9x11 + ... + 1/(2n-1)(2n+1)(2n+3)
我连起步都不会,参考书看没有。。救救我。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-5-2010 01:34 PM
|
显示全部楼层
发表于 15-5-2010 01:34 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-5-2010 01:35 PM
|
显示全部楼层
发表于 15-5-2010 01:35 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-5-2010 01:35 PM
|
显示全部楼层
发表于 15-5-2010 01:35 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-5-2010 02:54 PM
|
显示全部楼层
发表于 15-5-2010 02:54 PM
|
显示全部楼层
sequences and series:method of difference
到底怎么做啊?我一点idea也没有~
例如这题要怎么做呢?
...
道信 发表于 15-5-2010 01:28 PM 
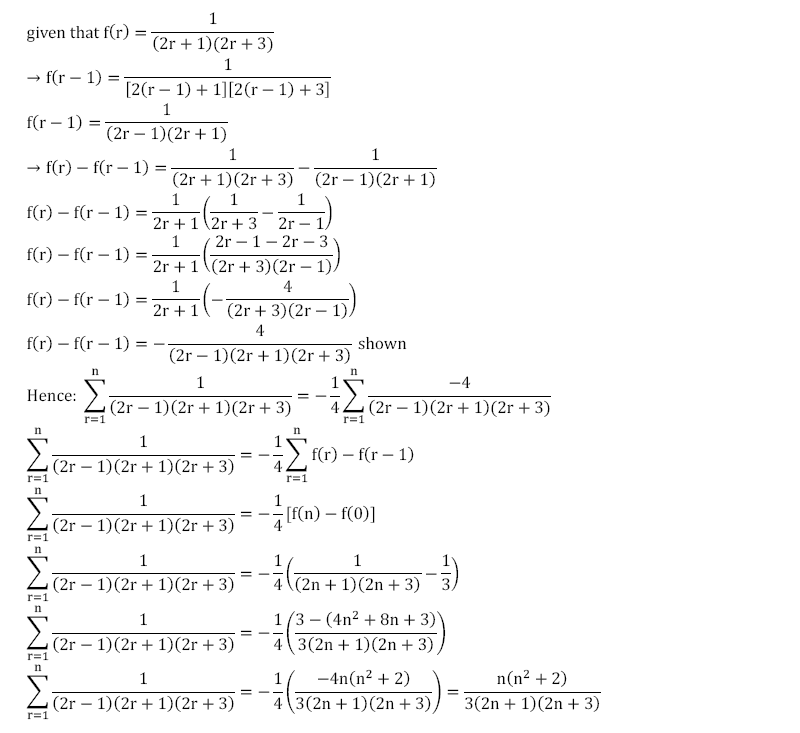 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-5-2010 10:27 PM
|
显示全部楼层
发表于 16-5-2010 10:27 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-5-2010 01:57 AM
|
显示全部楼层
发表于 17-5-2010 01:57 AM
|
显示全部楼层
回复 1058# whyyie
题目给你的那两条线的eqn
如果你拿来做simultaneous
你就会拿到拿个parallelogram ABCD的其中一个点了(let it be A)
然后你拿题目给的(point where the diagonal meets)是你的midpoint of the points forming the diagonal
so you can get point C now
then using one of the gradient of the 2 lines given just now and point C to form a new straight line eqn
then take this eqn intersect with the line which you didn't use with point C to form the straight line just now
you can get another point(let it be B) ady
last point
is D
midpoint of DB = midpoint of AC
done.. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-5-2010 03:59 PM
|
显示全部楼层
发表于 17-5-2010 03:59 PM
|
显示全部楼层
if a and b are not real number, then ab is also not a real number.
State whether the statement above true or false.
If false, give example. |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|