|
|
 发表于 4-5-2010 04:05 PM
|
显示全部楼层
发表于 4-5-2010 04:05 PM
|
显示全部楼层
P(x)=(x²-5x+6)Q(x) + (x+3)
= (x-3)(x-2)Q(x) +(x+3) --- (1)
P(x)=(x²-6x+8)Q(x)+(2x+1)
= (x-4)(x-2)Q(x)+(2x+1) -- (2)
P(x) =(x²-7x+12)Q(x)+( ax+b)
=(x-3)(x-4)Q(x)+ (ax+b) --- (3) 【Q(x) is quotient and are different for each】
(1)=(3),insert x=3, 6= 3a+b --- (4)
(2)=(3), insert x = 4, 9 = 4a+b--- (5)
solve ang get the remainder. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-5-2010 04:18 PM
|
显示全部楼层
发表于 4-5-2010 04:18 PM
|
显示全部楼层
回复 1016# walrein_lim88
应该是 x²
+(3a-2)x+a(a-1)=0
可是也没差,做法一样。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-5-2010 04:21 PM
|
显示全部楼层
发表于 4-5-2010 04:21 PM
|
显示全部楼层
奇怪
做么以上的问题我在chapter2没有做过的?
难道是别个chapter的?== |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-5-2010 05:33 PM
|
显示全部楼层
发表于 4-5-2010 05:33 PM
|
显示全部楼层
|
If the equation a^2+bx+c=0 has the roots A and B,find in terms of A and B, the roots of the equation (a^2)(y^2)-(b^2-2ac)y+c^2=0 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-5-2010 05:59 PM
|
显示全部楼层
发表于 4-5-2010 05:59 PM
|
显示全部楼层
本帖最后由 Log 于 4-5-2010 06:02 PM 编辑
回复 1024# Lov瑜瑜4ever
Given ax²+bx+c=0, roots : A, B
A+B= - b/a AB=c/a
-(A+B)= b/a
(a²)y²- (b²-2ac)y+c²=0 let the roots be p and q
p+q= -【- (b²-2ac)/a²】 pq=c²/a²
= b²/a² - 2ac/a² = (b/a)² - 2c/a =(c/a)²
= (A+B)² - 2AB pq=A²B²
p+q = A²+B² ---(1) q=A²B² /p ---- (2)
把 (2) into (1),and rearrange, u get p² - (A²+B²)p+(A²B² )=0c
(p-A²)(p-B²)=0
p = A² or p=B² and q=B² or q=A²
∴ the roots for second equation are A² and B². |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-5-2010 06:06 PM
|
显示全部楼层
发表于 4-5-2010 06:06 PM
|
显示全部楼层
回复 1023# Lov瑜瑜4ever
一样在chapter2的,问题嘛?可以千变万化的 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-5-2010 08:26 PM
|
显示全部楼层
发表于 4-5-2010 08:26 PM
|
显示全部楼层
回复 Lov瑜瑜4ever
Given ax²+bx+c=0, roots : A, B
A+B= - b/a AB=c/a
-(A+B)= b/a
...
Log 发表于 4-5-2010 05:59 PM 
噢噢
明白了 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-5-2010 08:27 PM
|
显示全部楼层
发表于 4-5-2010 08:27 PM
|
显示全部楼层
回复 Lov瑜瑜4ever
Given ax²+bx+c=0, roots : A, B
A+B= - b/a AB=c/a
-(A+B)= b/a
...
Log 发表于 4-5-2010 05:59 PM 
噢噢
明白了 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 12:29 PM
|
显示全部楼层
发表于 6-5-2010 12:29 PM
|
显示全部楼层
If the quadratic equations 3x^2+ax-1=0 and x^2+bx+2=0 where a and b are constants, have a common root, show that
2a^2-3b^2-5ab+49=0 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 12:46 PM
|
显示全部楼层
发表于 6-5-2010 12:46 PM
|
显示全部楼层
If the quadratic equations 3x^2+ax-1=0 and x^2+bx+2=0 where a and b are constants, have a common roo ...
Lov瑜瑜4ever 发表于 6-5-2010 12:29 PM 
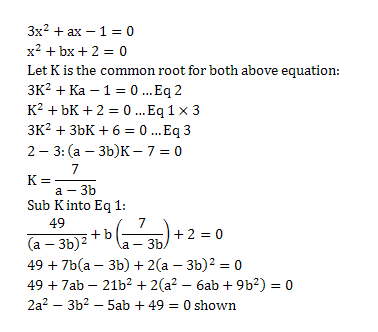 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 06:21 PM
|
显示全部楼层
发表于 6-5-2010 06:21 PM
|
显示全部楼层
我有几个问题想请教各位:
1)The equation 12x^4+20x^3-11x^2-5x+2=0 has one integer root. Find this root and hence, solve the equation completely.
书的答案是x=-2,1/3,+1/2,-1/2
2)如果要factorise上面的equation的话,在factorise的时候应该会得到类似这样的equation
12x^4+20x^3-11x^2-5x+2=0
(ax^2+bx+c)(dx^2+ex+f)=0
a,b,c,d,e,f是constant。a和d是12的factor,然后c和f是2的factor,那么要怎么得到a,d,c,f
的value.(这题不是书本里的) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 06:53 PM
|
显示全部楼层
发表于 6-5-2010 06:53 PM
|
显示全部楼层
我有几个问题想请教各位:
1)The equation 12x^4+20x^3-11x^2-5x+2=0 has one integer root. Find this r ...
blazex 发表于 6-5-2010 06:21 PM 
其实你的办法是不可能找到a和d的:
用这个办法来做:
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 07:19 PM
|
显示全部楼层
发表于 6-5-2010 07:19 PM
|
显示全部楼层
其实你的办法是不可能找到a和d的:
用这个办法来做:
walrein_lim88 发表于 6-5-2010 06:53 PM 
如果我不知道书里的答案,那么我应该怎样作答呢? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 07:24 PM
|
显示全部楼层
发表于 6-5-2010 07:24 PM
|
显示全部楼层
如果我不知道书里的答案,那么我应该怎样作答呢?
blazex 发表于 6-5-2010 07:19 PM 
其实是这样做的:如果degree > 2 .( 3 onwards)
1. guess 一个ROOT出来
如何猜呢? 看最后面那个CONSTANT,就刚才那题:
cosntant 是2: 那么我们就可以猜root 可以 1, 2 , -1 ,-2 ( one by one sub inside calculator)
猜出来后,factorise by 2 ways:
1. comparing coefficient.
2. long division
找出来后, 一样的: 如果第二个FACTOR还是 degree> 2
1. guess 出来
2. factorise again by comparing coefficient/ long division
就这样一直REPEAT
( note: for degree 3, instead of guessing, u can make a cheat to ur teacher by pressing calculator) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 07:40 PM
|
显示全部楼层
发表于 6-5-2010 07:40 PM
|
显示全部楼层
本帖最后由 Lov瑜瑜4ever 于 6-5-2010 08:21 PM 编辑
Prove without using a calculator, that
(a) 2<t<3 and deduce that 0<t-2<1,
(b) (t+2)^4+(t-2)^4=322,
(c) 321<(t+2)^4<322.
t=5^1/2 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 6-5-2010 08:27 PM
|
显示全部楼层
其实你的办法是不可能找到a和d的:
用这个办法来做:
walrein_lim88 发表于 6-5-2010 06:53 PM 
为什么不用newton-rapson 来找root?
找到一个root 过后 , 再用long division不是更快吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 08:31 PM
|
显示全部楼层
发表于 6-5-2010 08:31 PM
|
显示全部楼层
为什么不用newton-rapson 来找root?
找到一个root 过后 , 再用long division不是更快吗?
白羊座aries 发表于 6-5-2010 08:27 PM 
你说的是什么招式啊?
介绍来看看
哈哈 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 08:55 PM
|
显示全部楼层
发表于 6-5-2010 08:55 PM
|
显示全部楼层
本帖最后由 whyyie 于 6-5-2010 08:58 PM 编辑
回复 1035# Lov瑜瑜4ever

2<t<3
2-2<t-2<3-2
0<t-2<1 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 6-5-2010 08:58 PM
|
显示全部楼层
你说的是什么招式啊?
介绍来看看
哈哈
Lov瑜瑜4ever 发表于 6-5-2010 08:31 PM 
to determine the root of
12x^4+20x^3-11x^2-5x+2=0
dy/dx = 48x^3 +60x^2 -22x -5
using x = 0
dy/dx = -5 < 0
ok, now we have negative value, find 1 more value that is positive by subsitute any value of x into dy/dx
when x = -1
dy/dx = 29 >0 , positive
then the root must b lie on 0 and -1
by using newton-rapson law , choose any number that are in between 0 and -1 ,
let say 0.2,
then by tekankan calculator anda ,
x( root ) = x1 ( the number u assume, in this case i put 0.2) - f(x)/f'(x)
where f(x) = 12x^4+20x^3-11x^2-5x+2
and f'x = 48x^3 +60x^2 -22x -5
so f(0.2) and f'(0.2) , u will not yet get ur answer , then
x( root ) = x1 ( the previous answer u get ) -f(x)/f'(x)
by pressing enter on ur calculator only, till a constant value u get, that is first root, that is 1/3
then since u know 1/3 is root, that mean the equation must have (3x-1) , by using this , long division |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-5-2010 09:13 PM
|
显示全部楼层
发表于 6-5-2010 09:13 PM
|
显示全部楼层
to determine the root of
12x^4+20x^3-11x^2-5x+2=0
dy/dx = 48x^3 +60x^2 -22x -5
using ...
白羊座aries 发表于 6-5-2010 08:58 PM 
噢噢噢。。。 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|