|
|
 发表于 29-4-2010 09:13 PM
|
显示全部楼层
发表于 29-4-2010 09:13 PM
|
显示全部楼层
how to show 10^log x = x
f(x) = 10^x
g(x) = log x
show that fg(x) = gf(x)
各位大大帮帮忙,谢 ...
Razor_1130 发表于 29-4-2010 07:53 PM 
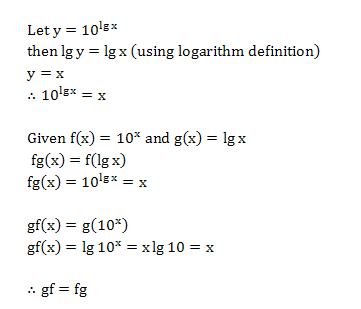 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-4-2010 09:18 PM
|
显示全部楼层
发表于 29-4-2010 09:18 PM
|
显示全部楼层
哦!let y = 10^log x
thxQ very much! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-4-2010 09:56 PM
|
显示全部楼层
发表于 29-4-2010 09:56 PM
|
显示全部楼层
据我所知, 零不能等于零, 所以x=y= 0 应该不算.
是书的答案吗? 你跟老师确定好了.
whyyie 发表于 29-4-2010 08:58 PM 
书本是这个答案
不过我以后还是会和老师确定下。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-4-2010 04:00 PM
|
显示全部楼层
发表于 30-4-2010 04:00 PM
|
显示全部楼层
这题怎么做??
A prize fund was set up with a single investment of RM2000 to provide an annual prize of RM150. The fund is given interest at 5% p.a. paid yearly. If the first prize was awarded one year after the investment, find the number of year for which the full prize can be awarded. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-4-2010 04:27 PM
|
显示全部楼层
发表于 30-4-2010 04:27 PM
|
显示全部楼层
Q1)x^2+xy=1/2(a)(a+b)
xy+y^2=1/2(a)(a-b)
a不等于0
HSC的问题来的
Q2) 2x+3y=1
2/x+3/y=1
这个有什么比较快的方法呢?
还是只能用substitution呢? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-4-2010 05:45 PM
|
显示全部楼层
发表于 30-4-2010 05:45 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-4-2010 06:35 PM
|
显示全部楼层
发表于 30-4-2010 06:35 PM
|
显示全部楼层
walrein_lim88 发表于 30-4-2010 05:45 PM 
有点复杂
哈哈
thx。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 09:32 AM
|
显示全部楼层
发表于 1-5-2010 09:32 AM
|
显示全部楼层
If p is a root of f(x)=0 and g(x)=0,
prove af(x)+bg(x)=0 where a and b is a constant.
My solution:
Let f(x)=(x-p)Q1(x),where Q1(x) is the remaining product of f(x)
g(x)=(x-p)Q2(x),where Q2(x) is the remaining product of g(x)
So, af(x)+bg(x)=(x-p)Q1(x)+(x-p)Q2(x)
Since p is the root of both equation
then substitute x=p into the af(x)+bg(x)
(p-p)Q1(x)+(p-p)Q2(x)=0
LHS=0 and RHS=0
Since LHS=RHS
The statement is proven
这样做可以的吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 11:49 AM
|
显示全部楼层
发表于 1-5-2010 11:49 AM
|
显示全部楼层
看到一个不懂要怎样下手的题目
Given that f(x)=x^n-nx+n-1 for the integer n>1
By considering f(x) and f'(x), show that
f(x)=[(x-1)^2]g(x)
is true for all polynomials g(x) with integer coefficients.
Hence, or otherwise (最好可以用Hence)
(i) show that 3^(2n)-8n-1 is divisible by 64 for all integers n>1
(ii) show that the equation
x^4-4x+3=0
does not have any real root other than 1.
(STPM 1993yrs,Math T)
幸好我没在那年考stpm
啊哈哈哈哈哈 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 12:46 PM
|
显示全部楼层
发表于 1-5-2010 12:46 PM
|
显示全部楼层
看到一个不懂要怎样下手的题目
Given that f(x)=x^n-nx+n-1 for the integer n>1
By considering f(x) an ...
Lov瑜瑜4ever 发表于 1-5-2010 11:49 AM 
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 12:47 PM
|
显示全部楼层
发表于 1-5-2010 12:47 PM
|
显示全部楼层
If p is a root of f(x)=0 and g(x)=0,
prove af(x)+bg(x)=0 where a and b is a constant.
My solutio ...
Lov瑜瑜4ever 发表于 1-5-2010 09:32 AM 
问题我觉得怪怪。。。af(x)+bg(x)=0
你的SOLUTION,只能PROVE到X=p罢了。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 01:02 PM
|
显示全部楼层
发表于 1-5-2010 01:02 PM
|
显示全部楼层
walrein_lim88 发表于 1-5-2010 12:46 PM 
你说的那个theoram不再syllabus里面了?
那时什么theoram来的?
你有看过吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 01:03 PM
|
显示全部楼层
发表于 1-5-2010 01:03 PM
|
显示全部楼层
问题我觉得怪怪。。。af(x)+bg(x)=0
你的SOLUTION,只能PROVE到X=p罢了。。。
walrein_lim88 发表于 1-5-2010 12:47 PM 
那如果是你
你要怎样证明勒? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 02:06 PM
|
显示全部楼层
发表于 1-5-2010 02:06 PM
|
显示全部楼层
你说的那个theoram不再syllabus里面了?
那时什么theoram来的?
你有看过吗?
Lov瑜瑜4ever 发表于 1-5-2010 01:02 PM 
这个THEOREM:
if both f(x) and f'(x) has the same roots k,
then f(x)=(x-k)^2 g(x) (有个SQUARE) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 02:07 PM
|
显示全部楼层
发表于 1-5-2010 02:07 PM
|
显示全部楼层
那如果是你
你要怎样证明勒?
Lov瑜瑜4ever 发表于 1-5-2010 01:03 PM 
我不知道。。觉得好像PROVE不到。。。除非题目改去这样:af(x) +bg(x)=0 for x=p..... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 02:38 PM
|
显示全部楼层
发表于 1-5-2010 02:38 PM
|
显示全部楼层
这个THEOREM:
if both f(x) and f'(x) has the same roots k,
then f(x)=(x-k)^2 g(x) (有 ...
walrein_lim88 发表于 1-5-2010 02:06 PM 
有关于这个theorem的证明吗?
我要看 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 02:40 PM
|
显示全部楼层
发表于 1-5-2010 02:40 PM
|
显示全部楼层
我不知道。。觉得好像PROVE不到。。。除非题目改去这样:af(x) +bg(x)=0 for x=p.....
walrein_lim88 发表于 1-5-2010 02:07 PM 
肯定是x=p的嘛
都说p是他们的root了
所以x当然等于p了咯 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 03:45 PM
|
显示全部楼层
发表于 1-5-2010 03:45 PM
|
显示全部楼层
show that, for y不等于0, the polynomial p(y)=y^6-2y^5-4y^4+6y^3+4y^2-2y-1 can be expressed as
p(y)=(y^3)(t^3-2t^2-t+2), where t=y-1/y
看下题目有错吗?
我做到的是p(y)=(y^3)(t^3-2t^2-t+8)哦。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 10:01 PM
|
显示全部楼层
发表于 1-5-2010 10:01 PM
|
显示全部楼层
肯定是x=p的嘛
都说p是他们的root了
所以x当然等于p了咯
Lov瑜瑜4ever 发表于 1-5-2010 02:40 PM 
没有啊。。。他只是说p is the root..
可是问题只PROVE f(x)
x = 可以很多VALUE除了P以外。。。。
毕竟问题没有RESTRICT DOMAIN
(我觉得啦) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 1-5-2010 10:02 PM
|
显示全部楼层
发表于 1-5-2010 10:02 PM
|
显示全部楼层
有关于这个theorem的证明吗?
我要看
Lov瑜瑜4ever 发表于 1-5-2010 02:38 PM 
我不会他这个THOEREM。。。只是在书上看到罢了~~ |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|