|
|
 发表于 11-3-2010 08:50 PM
|
显示全部楼层
发表于 11-3-2010 08:50 PM
|
显示全部楼层
回复 800# bushman_tong
LOL ..我不是老师。。。才考完STPM吧了。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-3-2010 09:02 PM
|
显示全部楼层
发表于 11-3-2010 09:02 PM
|
显示全部楼层
小弟在这儿想请教各位大哥大姐..
1)Given that n is a positive integer,
(a) Find in tern of S1, the sum of integers from 2n to 4n inclusive.
(b) Find in term of S2, the sum of odd integers from 2n to 4n.
2)Positive integers are grouped in brackets:
(1) , (2,3) , (4,5,6) ,.........with r integers in the rth bracket.
(a) Find the expression for the first and last term in the rth bracket.
(b) Find the sum of all the integers in the first 20 brackets.
(c) Prove that the sum of integers in the rth bracket is (r/2)[(r^2)+1]
希望各位可以帮到我..谢谢! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-3-2010 09:44 PM
|
显示全部楼层
发表于 11-3-2010 09:44 PM
|
显示全部楼层
回复 801# walrein_lim88
不好意思...误会了... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-3-2010 10:51 AM
|
显示全部楼层
发表于 12-3-2010 10:51 AM
|
显示全部楼层
回复 802# bushman_tong
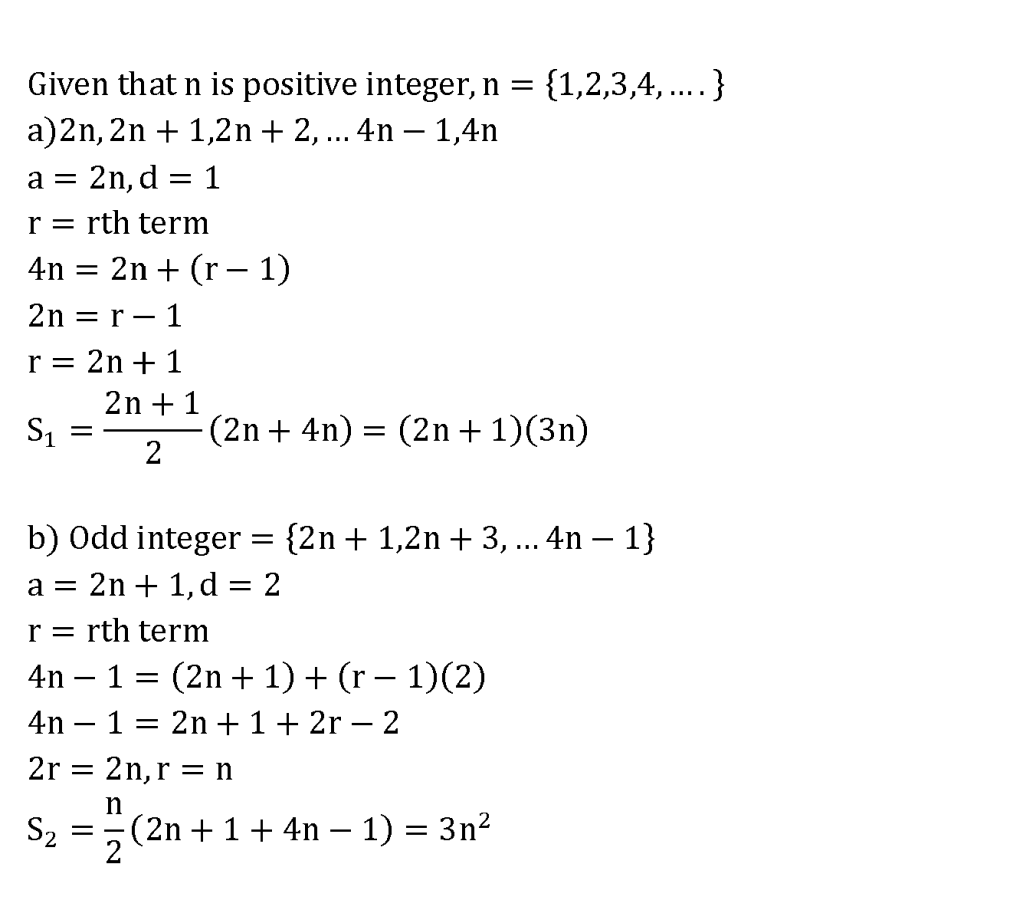 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-3-2010 11:25 AM
|
显示全部楼层
发表于 12-3-2010 11:25 AM
|
显示全部楼层
回复 802# bushman_tong
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-3-2010 10:01 PM
|
显示全部楼层
发表于 12-3-2010 10:01 PM
|
显示全部楼层
本帖最后由 bushman_tong 于 12-3-2010 10:05 PM 编辑
回复 805# walrein_lim88
小弟有不明之处...
如何找 An=1+(n/2)(1+n) ?
还有为什么last term in the rth bracket 要加 (r - 1)(1)? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-3-2010 10:25 PM
|
显示全部楼层
发表于 12-3-2010 10:25 PM
|
显示全部楼层
回复 806# bushman_tong
对不起。。我打错。。是Ar=1+0.5(r-1)(r)
解释:
注意下1st term for each bracket, there is a pattern:
1, 2, 4, 7, 11, 16....
+1 +2 +3 +4 +5..........
1st term: 1
2nd term is: 1 + (1) -is summation of AP
3rd term is : 1+ (1+2) summation of AP - look at the last term : r-1(3-1=2)
4th term is : 1 + (1+2+3) summation of AP look at last term: r-1 (4-1=3)
deduce that:
for 1st term for rth bracket:
1+ (1+2+3+..+r-1)
Use AP summation formula:
1+ 0.5(r-1)(r-1+1)=1+0.5(r-1)(r)
|
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-3-2010 10:28 PM
|
显示全部楼层
发表于 12-3-2010 10:28 PM
|
显示全部楼层
回复 806# bushman_tong
还有为什么last term in the rth bracket 要加 (r - 1)(1)?
现在我们知道。。for every 1st term in rth bracket:
=1+(0.5)(r-1)(r)
我们看下LAST TERM:
注意上面的PATTERN:
(1), (2,3),(4,5,6)
1st bracket = 1 term
2nd bracket = 2 term
3rd bracket = 3 terms
so..if rth bracket = got r terms
然后再注意下里面的号码,其实也是AP ,where d = 1
so in rth bracket, a=1+0.5(r-1)(r) and d = 1 and there are r terms totally
so the last term Tr= a+ (r-1)d
Tr=1+0.5(r-1)(r)+(r-1)(1) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-3-2010 12:09 PM
|
显示全部楼层
发表于 13-3-2010 12:09 PM
|
显示全部楼层
回复 808# walrein_lim88
好难理解的题目..
谢谢! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-3-2010 12:15 PM
|
显示全部楼层
发表于 13-3-2010 12:15 PM
|
显示全部楼层
回复 809# bushman_tong
你明白吗?? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-3-2010 02:10 PM
|
显示全部楼层
发表于 13-3-2010 02:10 PM
|
显示全部楼层
回复 810# walrein_lim88
勉强可以...
还需要更深入的思考... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-3-2010 08:19 PM
|
显示全部楼层
发表于 13-3-2010 08:19 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-3-2010 09:13 PM
|
显示全部楼层
发表于 13-3-2010 09:13 PM
|
显示全部楼层
我快崩溃了...sequences and series 很难阿!!!
bushman_tong 发表于 13-3-2010 08:19 PM 
中六好像没有东西是容易的咯~ |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-3-2010 09:32 PM
|
显示全部楼层
发表于 13-3-2010 09:32 PM
|
显示全部楼层
回复 813# silent91
可以这么说...不然很多人就不用酱辛苦了... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-3-2010 09:38 PM
|
显示全部楼层
发表于 13-3-2010 09:38 PM
|
显示全部楼层
回复 814# bushman_tong
还是不明白吗??? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-3-2010 11:14 PM
|
显示全部楼层
发表于 13-3-2010 11:14 PM
|
显示全部楼层
回复 815# walrein_lim88
半懂半不懂....
我还没到你所思考的境界...
现在做着sequences and series 也是要死要活... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-3-2010 01:41 AM
|
显示全部楼层
发表于 14-3-2010 01:41 AM
|
显示全部楼层
这题也是伤脑筋...
n
Find ∑ (n+1+2r) in term of n.
r=0 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-3-2010 08:52 AM
|
显示全部楼层
发表于 14-3-2010 08:52 AM
|
显示全部楼层
回复 817# bushman_tong
r = 0 > n+1
n
=n+1 + ∑ (n+1+2r)
1
n n n
=n+1 + ∑ n+∑1+2∑r)
1 1 1
n
=n+1+n^2+n+2∑ (r)
1
=n^2+n+1+2(n)(n+1)/2
=n^2+n+1+n^2+n
=2n^2+2n+1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-3-2010 10:07 AM
|
显示全部楼层
发表于 14-3-2010 10:07 AM
|
显示全部楼层

我校的math paper 1
第一课到coordinate geometry
答案要假期后才能给 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-3-2010 10:57 AM
|
显示全部楼层
发表于 14-3-2010 10:57 AM
|
显示全部楼层
回复 818# 芭樂
可是答案不是这个... |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|