|
|
 发表于 16-1-2010 10:33 PM
|
显示全部楼层
发表于 16-1-2010 10:33 PM
|
显示全部楼层
two parallel lines passes through (5,0) and (-5,0) respectively,they intersect with a straight line ...
數學神童 发表于 16-1-2010 09:28 PM 
还有可以用比较长的方法:
就是:
let y1=mx+c for point (5,0)
c=-5m
y1=mx-5m
y2=mx+5m( pass thru (-5,0))
den u do simultenous for both on the line 4x+3y=25 to get P and Q
den get the point P and Q, => do distance formula , then u get get m ald |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2010 10:35 PM
|
显示全部楼层
发表于 16-1-2010 10:35 PM
|
显示全部楼层
|
如果我用walrein_lim88的方法的话,我不是应该会得到两个大案吗?-4/7和4/7.但-4/7不是不正确的吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2010 10:38 PM
|
显示全部楼层
发表于 16-1-2010 10:38 PM
|
显示全部楼层
本帖最后由 walrein_lim88 于 16-1-2010 10:39 PM 编辑
如果我用walrein_lim88的方法的话,我不是应该会得到两个大案吗?-4/7和4/7.但-4/7不是不正确的吗?
數學神童 发表于 16-1-2010 10:35 PM 
上面已讲POSITIVE GRADIENT了,所以拿+ 足够。。(一定要画出来)
没有画会很乱
若不要画,用第二方法。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2010 10:41 PM
|
显示全部楼层
发表于 16-1-2010 10:41 PM
|
显示全部楼层
|
这题是PAST YEAR QUESTION,我做过的。。哈哈。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2010 10:51 PM
|
显示全部楼层
发表于 16-1-2010 10:51 PM
|
显示全部楼层
|
可是past year给的答案是4/7和-4/7。所以我就觉得confused。到底哪一个才是正确的答案? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2010 10:58 PM
|
显示全部楼层
发表于 16-1-2010 10:58 PM
|
显示全部楼层
可是past year给的答案是4/7和-4/7。所以我就觉得confused。到底哪一个才是正确的答案?
數學神童 发表于 16-1-2010 10:51 PM 
SINCE 我和四月的答案一样,那么-4/7应该是错的。。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-1-2010 11:32 PM
|
显示全部楼层
发表于 16-1-2010 11:32 PM
|
显示全部楼层
|
do the past year question got working?show us how it did,mayb we can solve it. |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-1-2010 09:56 PM
|
显示全部楼层
|
if y = e^-x/(1+x^2) , show tht (1+x^2)dy/dx +(1+x)^2y=0 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-1-2010 10:03 PM
|
显示全部楼层
发表于 19-1-2010 10:03 PM
|
显示全部楼层
本帖最后由 Log 于 19-1-2010 10:05 PM 编辑
白羊,
dy/dx={ (1+x^2)(-e^-x) - (e^-X)(2x)} / (1+x^2)^2
dy/dx = -e^-x / (1+x^2)^2 - 2xe^-x/ (1+x^2)^2
(1+x²)dy/dx= -e^-x - 2xe^-x/ (1+x²)
(1+x²)dy/dx= -e^-x [ 1+ 2x/(1+x²)]
k, for 1+ 2x/(1+x²)= (1+x)²/ (1+x²)
until here u can get |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-1-2010 10:05 PM
|
显示全部楼层
发表于 19-1-2010 10:05 PM
|
显示全部楼层
if y = e^-x/(1+x^2) , show tht (1+x^2)dy/dx +(1+x)^2y=0
白羊座aries 发表于 19-1-2010 09:56 PM 
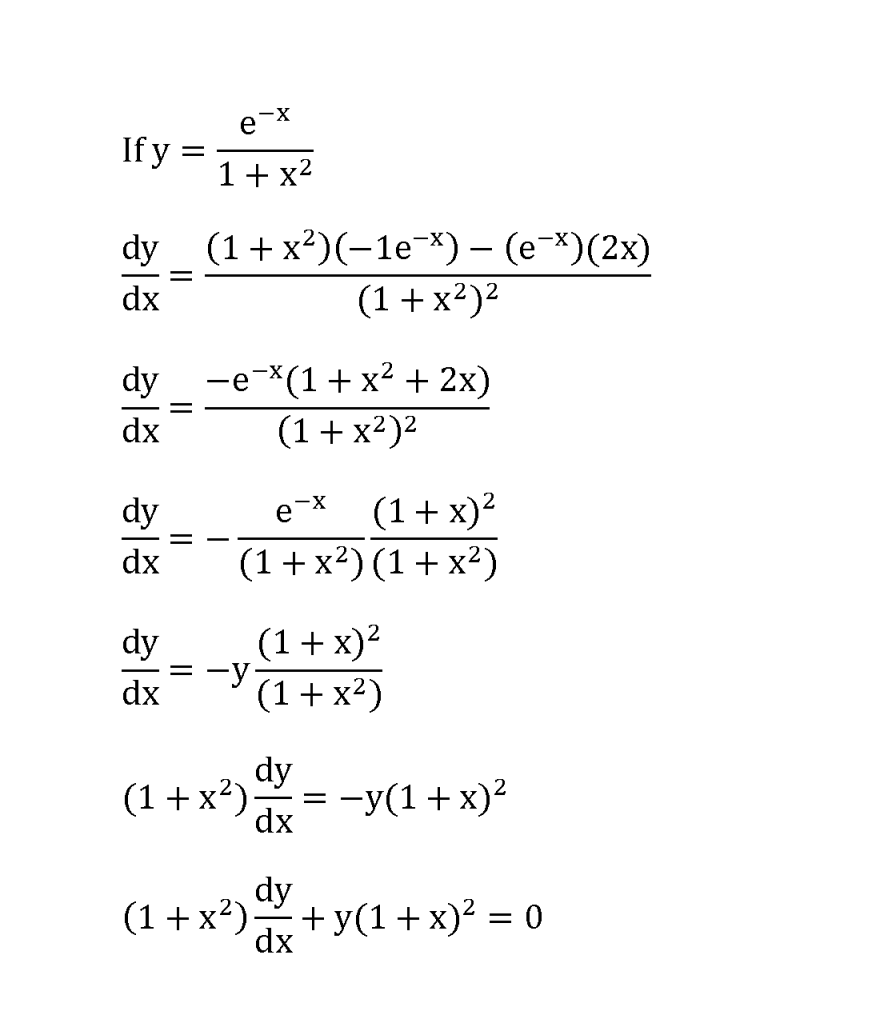 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-1-2010 10:13 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-1-2010 10:22 PM
|
显示全部楼层
发表于 19-1-2010 10:22 PM
|
显示全部楼层
请问还有别的做法吗?
用implicit的方法
白羊座aries 发表于 19-1-2010 10:13 PM 
implicit 不适合吧。。。会更乱而已。。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-1-2010 08:30 PM
|
显示全部楼层
y=1/2 (e^x+e^(-x) )show that (〖dy/dx)〗^2=y^2-1.
(e^x-e^(-x))/(e^x+e^(-x) ) show that dy/dx=1-y^2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-1-2010 08:44 PM
|
显示全部楼层
发表于 20-1-2010 08:44 PM
|
显示全部楼层
1. dy/dx= 1/2 (e^x-e^-x)
then, insert y into RHS
RHS=y^2-1
= {1/2 (e^x+e^-x)}² - 1
=1/4 (e^2x +2+e^-2x) - 1
= 1/4 e^2x -1/2 + 1/4e^-2x
=1/4 ( e^2x-2+e^-2x)
= 1/4(e^x-e^-x)²
= 【1/2 ( e^x-e^-x)】² = 【dy/dx】²
2. dy/dx = { (e^x+e^-x)(e^x+e^-x) - (e^x-e^-x)(e^x-e^-x) } / (e^x+e^-x)²
= { (e^x+e^-x) ² - (e^x-e^-x)² }/ (e^x+e^-x)²
= (e^x+e^-x) ²/ (e^x+e^-x) ² - (e^x-e^-x)² / (e^x+e^-x) ²
= 1 - 【(e^x-e^-x) / (e^x+e^-x) 】²
= 1- y² |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-1-2010 09:15 PM
|
显示全部楼层
differentiate x-tan x +1/3 tan^3 x with respect to x , express ur answer in terms of tan x
ans: tan^4 x |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-1-2010 09:28 PM
|
显示全部楼层
发表于 20-1-2010 09:28 PM
|
显示全部楼层
本帖最后由 Log 于 20-1-2010 10:39 PM 编辑
dy/dx= d(x)/dx- d(tanx)/dx +d( tan^3 x/ 3)/dx
= 1 -sec² x + tan^2 x . sec² x
= 1-1-tan^2 x + tan²x . (1+tan^2 x)
= tan^4 x |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-1-2010 09:44 PM
|
显示全部楼层
发表于 20-1-2010 09:44 PM
|
显示全部楼层
2x²y+6x=2x²+2 use quotient rule
divide by 2.so
x²y+3x=x²+1
y= x²-3x+1 / x²
dy/dx= x²(2x-3) - ( x²-3x+1)(2x) / x^4
=3x²-2x / x^4
dy/dx = 3x-2 / x³
x³dy/dx=3x-2 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-1-2010 10:42 PM
|
显示全部楼层
1.y= cos kx/ (1+ sin kx)
where k is positive integer
show that: cos kx d^2y/dx^2 =k^2y^2
2.x= 3 cos @-cos^3 @
y= 3 sin @-sin^3 @
express dy/dx in terms of @
@ = deta |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-1-2010 11:38 PM
|
显示全部楼层
发表于 25-1-2010 11:38 PM
|
显示全部楼层
1.y= cos kx/ (1+ sin kx)
where k is positive integer
show that: cos kx d^2y/dx^2 =k^2y^2
2.x ...
白羊座aries 发表于 25-1-2010 10:42 PM 
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-1-2010 11:38 PM
|
显示全部楼层
发表于 25-1-2010 11:38 PM
|
显示全部楼层
回复 698# 白羊座aries
1. y= cos kx / 1- sin kx = sec kx - tan kx 因为 multiply by 1-sin kx / 1-sin kx
then, 这就简单了。
dy/dx = k sec kx tan kx - k sec² kx
= k sec kx(tan kx -sec kx)
dy/dx = -ky sec kx ------(1)
d²y/dx²= -k [ sec kx.dy/dx +y.k sec kx tan kx]
= -k sec kx.dy/dx - k²y sec kx tan kx
from (1). substitute dy/dx
d²y/dx²=sec² kx - k²y sec kx tan kx
= k²y sec kx (sec kx - tan kx )
= k²y sec kx .y
= k²y²sec kx= k²y²/cos kx
so, cos kx d²y/dx²= k²y² |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|