|
|
 发表于 9-9-2009 03:03 PM
|
显示全部楼层
发表于 9-9-2009 03:03 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-9-2009 03:11 PM
|
显示全部楼层
发表于 9-9-2009 03:11 PM
|
显示全部楼层
回复 421# lonely_world 的帖子
U shaped quadrant ll for both this graphs k? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-9-2009 03:13 PM
|
显示全部楼层
发表于 9-9-2009 03:13 PM
|
显示全部楼层
原帖由 Log 于 9-9-2009 03:11 PM 发表 
U shaped quadrant ll for both this graphs k?
一个有过x axis..一个没有?
酱的话..另外一个的min point 不是不对了? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-9-2009 03:21 PM
|
显示全部楼层
发表于 9-9-2009 03:21 PM
|
显示全部楼层
yes 就是不一样min pont!这是因为values for a b and c in D>0 and D<0 not same |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-9-2009 03:49 PM
|
显示全部楼层
发表于 9-9-2009 03:49 PM
|
显示全部楼层
let y = -∆/4a
∆ > 0
-∆ < 0
-∆/4a < 0
y < 0
let y=-∆/4a
∆ < 0
-∆ > 0
-∆/4a > 0
y > 0 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-9-2009 08:51 PM
|
显示全部楼层
发表于 9-9-2009 08:51 PM
|
显示全部楼层
a point Q lies on the curve xy=12 and O is the origin. Find the equation of the locus of the midpoint of OQ.
有谁可以教教下吗?
我不知道要怎样做到答案那边。
(答案:xy=3) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-9-2009 05:28 PM
|
显示全部楼层
发表于 11-9-2009 05:28 PM
|
显示全部楼层
好像是这样做。。
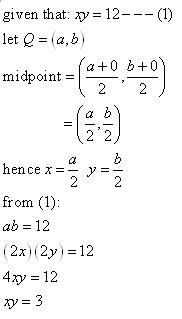 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-9-2009 04:46 AM
|
显示全部楼层
发表于 13-9-2009 04:46 AM
|
显示全部楼层
P(ap^2,2ap) and Q(aq^2,2aq) are points on the parabola y^2=4ax and PQ passes through the fixed point (a,0) ; PR and QR are parallel to the x-axis and y-axis respectively ; show that the locus of R has equation xy^2=4a^3
the tangent at P(ap^2,2ap),a point on the parabola y^2=4ax,meets the x-axis at T and S is the fixed point (a,0) ; show that SP=ST
P(ap^2,2ap) and Q(aq^2,2aq) are points on the parabola y^2=4ax and q=2p
TP and TQ are tangent to the parabola,show that the locus of T has the equation 2y^2=9ax

我明白问题问什么,但是不知道从哪里开始啊,快疯了
[ 本帖最后由 nkrealman 于 13-9-2009 06:30 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-9-2009 02:22 PM
|
显示全部楼层
发表于 13-9-2009 02:22 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-9-2009 02:22 PM
|
显示全部楼层
发表于 13-9-2009 02:22 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-9-2009 05:57 PM
|
显示全部楼层
发表于 13-9-2009 05:57 PM
|
显示全部楼层
P(ap^2,2ap) and Q(aq^2,2aq) are points on the parabola y^2=4ax and PQpasses through the fixed point (a,0) ; PQ and OR are parallel to thex-axis and y-axis respectively ; show that the locus of R has equationxy^2=4a^3
OR是什么来的?是不是the fixed point (a,0)? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-9-2009 06:19 PM
|
显示全部楼层
发表于 13-9-2009 06:19 PM
|
显示全部楼层
打错了,是PR和QR才对
[ 本帖最后由 nkrealman 于 13-9-2009 06:29 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-9-2009 06:28 PM
|
显示全部楼层
发表于 13-9-2009 06:28 PM
|
显示全部楼层
不知道我做的对不对。
我找 gradient of PQ,然后找equation of PQ
因为他passes through (a,0) 所以放进去找到 pq=-1
PR and QR are parallel to the x-axis and y-axis respectively
是不是说他们是perpendicular to each other?
我用他们两个的gradient乘起来=-1
找不到答案,是不是方法错了?
接下来那两题都不知道怎样做 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-9-2009 06:55 PM
|
显示全部楼层
发表于 14-9-2009 06:55 PM
|
显示全部楼层
|
zzzzzzzzz.....今天的数学paper 1很难=.=" |
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-9-2009 02:58 PM
|
显示全部楼层
发表于 15-9-2009 02:58 PM
|
显示全部楼层
原帖由 nkrealman 于 13-9-2009 04:46 AM 发表 
P(ap^2,2ap) and Q(aq^2,2aq) are points on the parabola y^2=4ax and PQ passes through the fixed point (a,0) ; PR and QR are parallel to the x-axis and y-axis respectively ; show that the locus of R has ...
PR parallel to x-axis,and QR parallel to y-axis
----> R (aq^2,2ap)
PQ : (p+q)y = 2(x + apq)
when y=0, x=a, pq = -1
let x=aq^2 and y=2ap
x=a(-1/p)^2 = a/(p^2) ...................1
y^2 = 4(a^2)(p^2)..........................2
2x1: x(y^2) = 4(a^3) ...(proven)
let (y^2) = 4ax
differentiate ---> 2y(dy/dx)=4a
(dy/dx)=2a/y .....................>gradient of tangent
at P,when y=2ap,
(dy/dx)=2a/2ap = 1/p
eqn: py = x + a(p^2)
when y = 0, x= -a(p^2)...........> T(-a(p^2),0)
(SP)^2= (ap^2- a)^2 + (2ap - 0)^2
= (ap^2)^2 - 2(ap)^2 + a^2 +4(ap)^2
= (ap^2)^2 + 2(ap)^2 + a^2
= (ap^2 + a)^2 = (a+ ap^2)^2
= (a - (-ap^2))^2
= (ST)^2
SP = ST |
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-9-2009 03:02 PM
|
显示全部楼层
发表于 15-9-2009 03:02 PM
|
显示全部楼层
P(ap^2,2ap) and Q(aq^2,2aq) are points on the parabola y^2=4ax and q=2p
TP and TQ are tangent to the parabola,show that the locus of T has the equation 2y^2=9ax
先把gradient of tangent of P and Q找出来。
然后form equation of P and Q。
T是point of intersection of equation of P AND Q。
找出T,然后就找出 locus of T,必要时用q=2p |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-9-2009 09:52 PM
|
显示全部楼层
发表于 26-9-2009 09:52 PM
|
显示全部楼层
1.( lx+3l +1)/( lx+3l -1)< 4
2.( lxl +3)/( lxl -3)>5
3.f(x)=x^4 -(p+1)x^2 +p
find set of values of p such that f(x) +2x^2 -2=0 has real and distinct root.
4.deduce that if m+ni is a root of ax^2 +bx +c=0 ,then m-ni is another root.
怎样做?
答案∶
1. -3<x<-2 or x>-4/3
2. -9/2<x<-3 or 3<x<9/2
3. p>2 and p not equal to 3 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-9-2009 02:20 PM
|
显示全部楼层
发表于 28-9-2009 02:20 PM
|
显示全部楼层
把4 搬过去减,
然后变成一个整分数后,
用=0的几个interval,
test是正还是负。
第二题也是。
第三题是把f(x)+2x^2 -2 后的quadratic equation
用b^2 - 4ac >0。
第四题是用derive quadratic formula的方法去算,
最后会算到那两个答案其实是conjugate to each other.
m = -b/2a , (+-) ni = i x determinant. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-10-2009 09:40 AM
|
显示全部楼层
发表于 4-10-2009 09:40 AM
|
显示全部楼层
回复 438# idontwant2b 的帖子
|
第三题能用quadratic equation吗?f(x)是quartic equation...用这个方法会找到P>3而不是P>2 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 4-10-2009 10:37 AM
|
显示全部楼层
原帖由 idontwant2b 于 28-9-2009 02:20 PM 发表 
把4 搬过去减,
然后变成一个整分数后,
用=0的几个interval,
test是正还是负。
第二题也是。
第三题是把f(x)+2x^2 -2 后的quadratic equation
用b^2 - 4ac >0。
第四题是用derive quadratic formula的方法去 ...
第4题不明白.. |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|