|
查看: 2730|回复: 9
|
dx和∆x和δx有什么分别?
[复制链接]
|
|
|
 发表于 21-8-2011 12:34 AM
|
显示全部楼层
发表于 21-8-2011 12:34 AM
|
显示全部楼层
根據我的了解
dx:這個是微分運算
∆x和δx:表示很小的x
當lim δx->0就可以定義dx |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 21-8-2011 01:26 AM
|
显示全部楼层
回复 2# puangenlun
所以δx和∆x是一样的? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-8-2011 08:22 AM
|
显示全部楼层
发表于 21-8-2011 08:22 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-8-2011 10:33 AM
|
显示全部楼层
发表于 21-8-2011 10:33 AM
|
显示全部楼层
δx 是 一个x1和x2之间的小差异/小相差。(a small change in x)
dx 是微分 (differentiate x)
dx/dy (differentiate x with respect to y)
dy = lim f(x+δx) - f(x)
dx δx->0 δx
|
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-8-2011 06:36 PM
|
显示全部楼层
发表于 21-8-2011 06:36 PM
|
显示全部楼层
本帖最后由 Scoutfai 于 21-8-2011 08:12 PM 编辑
我分享我的“讲错不负责任"自习成果,对于dx, Δx 和 δx 的见解。嗯,我也希望有人会指点我讲错的地方。
在single variable的讨论范围类,定义f为一个 real function,y为dependent variable, x为independent variable的话:
y = f(x) (任何时候都可以这样写)
平常,Δx和δx都一样,作者喜好而以。意即 Δx = δx 。Δ和δ都表示change of ?? , Δx和δx 就是change of x。Change就是 final value minus initial value。接着,看以下的图:

所以, Δx = δx = x_2 - x_1
因为 f(x_1) = y_1 , f(x_2) = y_2 , 所以, Δy = δy = y_2 - y_1 = f(x_2) - f(x_1)
因此, 任何Δ或 δ 的term 都有一个real value (你可能知道,可能不知道,看情况)。
通常,当x_2 - x_1是小的时候,人们用δx;大的时候,人们用Δx。怎样才算是大,才算是小呢?没有定论,看你心情。
Δx是比较通用的,因为δ(不是δx)这个符号在calculus通常被用在epsilon-delta definition of limit。
dx, 单单一个这样的写法,包含两个相近但不一样的概念。第一个是普通calculus认知里的infinitesimal(无限小),可以被称为differential。第二个是linear approximation里的dx, 也被称为differential(在这个应用领域里,不称它为infinitesimal)。
先谈第二个。
在calculus的differentiation里,first derivative可以被写成 dy/dx 或 f '(x) 或 df/dx,而它的定义是:
 (定义1) (定义1)
dy/dx 是 Leibniz notation。 dy/dx 是一个个体,不是dy除于dx。dy和dx在这里,没有被定义过,不具备任何意义。若在此阶段有人主张dy/dx 是一个 fraction,那么,它也可以被写成 (dy)/(dx),但也一样的,(dy)和(dx)从来没被定义过,所以不是 fraction。在定义first derivative的过程里,只需用到limit,Δy和Δx ,不需用到单单一个dy和dx。
那么,为了防止误会,我现在开始将first derivative写成 f '(x)而已。
differential of x, dx 是被定义为change of x, 就是说 dx=Δx。也就是说,dx,也是一个有real value的independent variable (所以就不是什么infinitesimal)。
differential of y, dy却是不一样的定义,dy的定义是:
 (定义2) (定义2)
因为dy是f '(x) (一个real value variable)和 dx (一个real value variable)的乘积,所以 dy 也是一个 real value dependent variable (所以就不是什么infinitesimal)。

从以上的图可以清楚看到dy和Δy的分别。dy可以大过,小过,或等于Δy。
Δy是change of y due to a change of x。dy是rise of the tangent line due to the same change in x (dx=Δx)。
定义2的等式被拿来用作approximation,尤其是当dx或Δx很小的时候(但这个不是必须的条件)。
同样的方法,在multiple variable案例时,意即 u = f (x, y, z), df, 这时被称作total differential, 是定义为:

Generally, 当z = z(x_1, x_2, x_3, ... ... , x_p) 时, total differential of z, dz 是:

这些等式都是被拿来用在linear approximation上。
若有注意到,其实differential of y, dy的等式(定义2)和f(x)的approximation差不多:
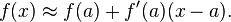
所以 f(x) - f(a) ≈ f '(a) * (x-a) , f(x) - f(a) = Δy , x-a = Δx , hence Δy ≈ f '(a)Δx , 不是跟定义2很像吗?
第二个在此完毕。
现在谈第一个。
Calculus一开始是被Newton和Leibniz各自独立创造的。两个天才都是在无限小(infinitesimal, dx,也被称为differential)这个概念上开始。Infinitesimal 就是infinitely small。但infinitesimal, dx的概念在Newton和Leibniz之前就有了一个不严谨定义:在Archimedes的书里,一个看起来严谨的infinitesimal定义被他提出,那就是:
“Archimediean property defines a number x as infinite if it satisfies the conditions |x|>1, |x|>1+1, |x|>1+1+1, ..., and infinitesimal if x≠0 and a similar set of conditions holds for 1/x and the reciprocals of the positive integers."
Speaking in heuristic term, dx 可以被当成是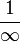 。但同时候,dx ≠ 0, dx只是 dx → 0 。但同时候,dx ≠ 0, dx只是 dx → 0
很明显,infinitesimal,dx不是一个real number。它不存在在set of real number。所以它没有real value。人们无法定义infinitesimal的arithmetic operation的,因为人们也无法在real number系统上定义∞的加减乘除。infinitesimal, dx和∞一样,是一个概念。
如果infinitesimal不是real number, 那么怎么可以写一些这样的式子呢,如 x+dx ? 严谨来说,在real analysis上是不对的。可是,利用这个错误的做法,却时常可以导出正确的成果。Leibniz和Newton的年代还没有limit的概念,他们就这样不管它是一个错误的用法,发展出了正确的calculus成果。Leibniz说过:“differentials (infinitesimals),it will be sufficient to simply make use of them as a tool that has advantages for the purpose of calculation, just as the algebraist retain imaginary roots with great profit.”
用infinitesimal, dx来发展calculus是受到某些严谨数学家的严厉批评的。例子:
y=x^2, 要找slope at x。用infinitesimal的方法,让e是一个infinitesimal(就是differential啦,只是不写成de而已)
slope = [ (x+e)^2 - x^2 ] / [ (x+e) - x ] = 2x + e
然后我们就会argue说因为e是无限小,比起2x,微不足道,所以可以cancelled, 因此 slope = 2x
答案是对,但方法呢?有矛盾吗?一开始e是不等于零,到最后却又可以变零。现在这情况还可以用intuition来认为最后变零无大碍,但当情况复杂化,人们又怎样判断呢?哲学家George Berkeley称这个e为the ghost of departed quantities。
讲回Leibniz那里。既然dx被Leibniz当作是一个无限小的change of x,那么,因为这个change of x而导致的change of y,也是无限小,被称为dy咯。所以Leibniz就很方便且毫无抗拒的将 f '(x) = dy/dx, 这里,Leibniz确实是当作fraction来看待。但就如以上说陈述的,成果对,方法不对(只从real analysis角度去看)。但又无可否认的,用这个错方法,很多calculus的formula都很容易被导出来喔,如chain rule, integration里的解释也变得很简单,非常intuitive。真的令数学家又爱又恨。
但在Cauchy和Karl Weierstrass发展出limit (epsilon-delta definition of limit)的概念后,infinitesimal就逐渐从主流数学被淘汰。现在所有的calculus, formally都是以limit为基础,没有用infinitesimal了。但在教学上,infinitesimal还是被用作一个heuristic, pedagogical tool of teaching,intuitive way of understanding。这些都是在不formal的情况下用而已,亦即嘴巴讲给你听而已,写在报告论文上还是回到limit。
可是,故事没有就此结束。
在1960,Abraham Robinson 将real number system 广张 (extend),将infinitesimal严谨的定义并收入进去广张了的number system,这个system就叫成hyperreal, 用hyperreal来研究的叫non-standard analysis。因为1/dx就变成infinity了,所以infinity也在hyperreal 里面。在这个领域,infinitesimal, or differential, dx是一个跟我们直觉的无限小接近,但不完全一样的东西。要用到non-standard analysis里的differential, dx是使用很不一样的手法的(我只知道不一样,不懂几不一样)。利用hyperreal,也可以导出回那些被Leibniz用dx导出来的成果,但Robinson的是严谨,Leibniz的是有逻辑漏洞存在的(他只是不去理会)。因为hyperreal, dx又回到了严谨数学的怀抱里。
因为hyperreal是一个极少被人使用的领域,几乎就只有纯数学家使用,所以当普通的calculus书里讲到dx,dy时,多是指定义2的等式和用法,不是指infinitesimal。但,要找出将dx,dy当作infinitesimal来用,却又没有介绍non-standard analysis给读者的书,也很容易,市面上充斥太多这样的书本,这类书本,或人士,这样使用infinitesimal是一种ill concept来的,但却可以启发式的教导读者,唯读者应该有这样的觉悟,王道的做法始终是用limit。
-----------------------------
总结,
在现代主流严谨calculus里,dx = δx = Δx = change of x , 但 dy ≠ δy, Δy , δy = Δy = change of y 。全部都有real value。
在非官方式里, dx = infinitesimal, 没有real value。 dx≠0 , 但 dx → 0 。也可以说 当
当 δx→ 0, δx = dx ≠ 0
当 Δx→ 0, Δx = dx ≠ 0 (δx,Δx一样的啦,写给网友看而已)
也曾经看过人主张
lim_(δx→ 0) { δx } = dx
这个我目前不认同,因为 δx = Δx 都只不过是real variable, 而
lim_(x→ 0) {x} = 0
但 dx≠0,所以我不认同。
虽然没被hyperreal处理的infinitesimal, dx是一个ill concept,但很多工程师,科学家都是这样用它来导出公式,而多数时候都对。这就如Leibniz讲的,暂时放弃严谨要求,把这个ill concept当作一个tool来用。导出结果后,再请纯数学家用limit证明回出来。
好了,完毕。请指教。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-8-2011 01:45 AM
|
显示全部楼层
发表于 22-8-2011 01:45 AM
|
显示全部楼层
我分享我的“讲错不负责任"自习成果,对于dx, Δx 和 δx 的见解。嗯,我也希望有人会指点我讲错的地方。
...
Scoutfai 发表于 21-8-2011 06:36 PM 
您真的是让我大开眼界~
请问您有什么书本好介绍让我们能够得到一些非官方,但真正有意思的书呢? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-8-2011 10:50 AM
|
显示全部楼层
发表于 22-8-2011 10:50 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 23-8-2011 10:37 PM
|
显示全部楼层
发表于 23-8-2011 10:37 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-8-2011 11:50 PM
|
显示全部楼层
发表于 25-8-2011 11:50 PM
|
显示全部楼层
delta 是很小的意思
三角形是两个点的差别
d是derivative |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|