|
|
本帖最后由 50912cmea 于 20-7-2019 07:10 PM 编辑
... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-6-2010 02:06 PM
|
显示全部楼层
发表于 11-6-2010 02:06 PM
|
显示全部楼层
本帖最后由 多普勒效应 于 11-6-2010 02:08 PM 编辑
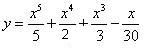 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-6-2010 07:31 PM
|
显示全部楼层
发表于 11-6-2010 07:31 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 11-6-2010 11:47 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-6-2010 12:00 AM
|
显示全部楼层
发表于 12-6-2010 12:00 AM
|
显示全部楼层
|
我也想问 50912cmea 您这个 function 有何意思? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-6-2010 02:36 AM
|
显示全部楼层
本帖最后由 50912cmea 于 20-7-2019 07:07 PM 编辑
... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-6-2010 08:00 AM
|
显示全部楼层
发表于 12-6-2010 08:00 AM
|
显示全部楼层
抱歉, 更希望您问"之前?",这个方程式的第一部分, (x^5)/5是Fermat先生提供的, 是 area under parabola ...
50912cmea 发表于 12-6-2010 02:36 AM 
老实说,不懂你在讲什么,可能我比你更猪脑吧...还是你可以更详细的解释... |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-6-2010 12:44 PM
|
显示全部楼层
本帖最后由 50912cmea 于 20-7-2019 07:07 PM 编辑
... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-6-2010 04:50 PM
|
显示全部楼层
发表于 13-6-2010 04:50 PM
|
显示全部楼层
回复 8# 50912cmea
50912cmea 你是读大专的吗???你的东西我没看过... 不好意思 不好意思 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-6-2010 10:46 PM
|
显示全部楼层
发表于 13-6-2010 10:46 PM
|
显示全部楼层
很漂亮的function..
Sum of the cubes of the first n natural numbers... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-6-2010 12:23 AM
|
显示全部楼层
发表于 14-6-2010 12:23 AM
|
显示全部楼层
原来这个equation (n^2)/4 (n+1)^2 是酱出来的...我之前研究这个equation的时候总是不明白...多谢这位楼主的分享,小弟收益不浅 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-6-2010 12:43 AM
|
显示全部楼层
发表于 14-6-2010 12:43 AM
|
显示全部楼层
|
楼主你的sum of the power of 4 of 1st n natural number的equation已经得证了吗??? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-6-2010 07:33 AM
|
显示全部楼层
发表于 14-6-2010 07:33 AM
|
显示全部楼层
∑n = 1 + 2 + 3 + ... ... + (n-1) + n
∑n = n + (n-1) + ... ... + 3 + 2 + 1
2∑n = (n+1) + (n+1) + (n+1) + ... ... + (n+1)
∑n = n(n+1)/2
(n+1)^3 = n^3 + 3n^2 + 3n + 1
n^3 = (n-1)^3 + 3(n-1)^2 + 3(n-1) + 1
(n-1)^3 = (n-2)^3 + 3(n-2)^2 + 3(n-2) + 1
(n-2)^3 = (n-3)^3 + 3(n-3)^2 + 3(n-3) + 1
...
...
3^3 = 2^3 + 3·2^2 + 3·2 + 1
2^3 = 1^3 + 3·1^2 + 3·1 + 1
各式两边相加后消去相同的项:
(n+1)^3 = 1 + 3∑n^2 + 3∑n + n
整理得:
∑n^2 = n(n+1)(2n+1)/6
(n+1)^4 = n^4 + 4n^3 + 6n^2 + 4n + 1
n^4 = (n-1)^4 + 4(n-1)^3 + 6(n-1)^2 + 4(n-1) + 1
(n-1)^4 = (n-2)^4 + 4(n-2)^3 + 6(n-2)^2 + 4(n-2) + 1
(n-2)^4 = (n-3)^4 + 4(n-3)^3 + 6(n-3)^2 + 4(n-3) + 1
...
...
3^4 = 2^4 + 4·2^3 + 6·2^2 + 4·2 + 1
2^4 = 1^4 + 4·1^3 + 6·1^2 + 4·1 + 1
各式两边相加后消去相同的项:
(n+1)^4 = 1 + 4∑n^3 + 6∑n^2 + 4∑n + n
整理得:
∑n^3 = n^2 (n+1)^2/4
同样的,
(n+1)^5 = n^5 + 5n^4 + 10n^3 + 10n^2 + 5n + 1
n^5 = (n-1)^5 + 5(n-1)^4 + 10(n-1)^3 + 10(n-1)^2 + 5(n-1) + 1
(n-1)^5 = (n-2)^5 + 5(n-2)^4 + 10(n-2)^3 + 10(n-2)^2 + 5(n-2) + 1
(n-2)^5 = (n-3)^5 + 5(n-3)^4 + 10(n-3)^3 + 10(n-3)^2 + 5(n-3) + 1
...
...
3^5 = 2^5 + 5·2^4 + 10·2^3 + 10·2^2 + 5·2 + 1
2^5 = 1^5 + 5·1^4 + 10·1^3 + 10·1^2 + 5·1 + 1
各式两边相加后消去相同的项:
(n+1)^5 = 1 + 5∑n^4 + 10∑n^3 + 10∑n^2 + 5∑n + n
整理得:
∑n^4 = ... ... |
评分
-
查看全部评分
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-6-2010 05:00 PM
|
显示全部楼层
发表于 14-6-2010 05:00 PM
|
显示全部楼层
回复 8# 50912cmea
b和c是不是猜的?
还是你有什么方法? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-6-2010 05:02 PM
|
显示全部楼层
发表于 14-6-2010 05:02 PM
|
显示全部楼层
回复 13# mathlim
我看华罗庚的《从杨辉三角谈起》
有一个比较简单且一般的方法 |
评分
-
查看全部评分
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 14-6-2010 06:34 PM
|
显示全部楼层
本帖最后由 50912cmea 于 20-7-2019 07:07 PM 编辑
... |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 14-6-2010 07:22 PM
|
显示全部楼层
本帖最后由 50912cmea 于 20-7-2019 07:07 PM 编辑
... |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 14-6-2010 07:36 PM
|
显示全部楼层
本帖最后由 50912cmea 于 20-7-2019 07:08 PM 编辑
... |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 14-6-2010 08:04 PM
|
显示全部楼层
本帖最后由 50912cmea 于 20-7-2019 07:08 PM 编辑
... |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 14-6-2010 08:21 PM
|
显示全部楼层
本帖最后由 50912cmea 于 20-7-2019 07:08 PM 编辑
... |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|